
L'Alphabet des Cathédrales
Dans ces quatre feuilles il y a des figures de l’art de géométrie, mais celui qui veut savoir laquelle il doit utiliser, convient avoir un grand égard pour les connaitre.
Villard de Honnecourt
Il est temps de découvrir les figures géométriques utilisées par les architectes médiévaux. Elles sont étonnamment simples et peu nombreuses.
Pour cela, je vais partir d'un dicton issu de la Bauhütte, l’organisation qui fédérait les loges de tailleurs de pierre du Saint-Empire romain germanique.
Un point dans le cercle,
Et qui se place dans le carré et le triangle.
Connais-tu ce point ? Tout est bien,
Ne le connais-tu pas ? Tout est vain.
Cette charade semble contenir sous une forme ésotérique un tour de main de traçage. On y retrouve les principales figures des tracés gothiques. Aussi, et pour que tout ne soit pas « vain », allons-nous débuter par le premier vers de ce poème et planter la pointe de notre compas. D'un geste faisons surgir le cercle, une spirale dans le temps.
Je viens de tracer la figure géométrique primordiale, la genèse de toute architecture sacrée. Impossible de résumer son champ d'application tant il est vaste. De la coupole à l'arc plein-cintre en passant par les déambulatoires ou l'arc gothique, le cercle s'incarne dans toutes les techniques. De même l'ensemble des figures régulières s'inscrivent dans sa circonférence.
Passons au deuxième vers « Le point se place dans le triangle », figure qui pour Viollet-le-Duc est « entièrement satisfaisante, parfaite, en ce qu'elle donne l'idée la plus exacte de la stabilité. »
Quand il forme un angle droit, il est rectangle et s'associe à l’équerre. Sur le chantier, les compagnons l'obtiennent à l'aide d'une corde divisée par des nœuds. Cette corde, également appelée corde des druides ou corde égyptienne, est séparée en douze espaces égaux par treize nœuds ayant chacun la valeur d’une coudée. Voyez-la comme une chaine d'arpenteur.
Prenons par exemple le triangle dit « de Pythagore ». Constitué d'un côté de 3 unités, d'un autre de 4, et d'une hypoténuse de 5, il forme un triangle rectangle, le premier à être généré par une série arithmétique. On voit qu'il permet de poser des axes, de créer un quadrillage. Cette opération reste à l'origine de tout travail et légitime la place privilégiée de l’équerre dans les symboles utilisés par les maçonneries et les compagnonnages. À cet instrument peut se substituer la règle et le compas. Ainsi, disposant d'une simple droite, il suffira de tracer deux arcs de cercle symétriques pour pouvoir tracer une médiatrice. En reliant ces trois points on obtient le triangle à trois côtés égaux, le triangle équilatéral. Ce triangle, connu de tous les écoliers, va me permettre d'introduire les tracés d'arcs gothiques. En effet, non content de trôner au centre des cathédrales, le triangle équilatéral permet de dessiner les ogives qualifiées de « tiers-points ».
Pour cela, il nous faut étudier les différentes formes d'arcs utilisés par les bâtisseurs médiévaux. Dans son carnet de notes, Villard de Honnecourt nous montre comment les dessiner, et ce, avec une seule ouverture de compas (fig. 3a).

Fig. 3a - Tracés d'arcs brisés (Villard de Honnecourt - folio 41)
En premier lieu, on aperçoit un arc en plein cintre (fig. 3b). Il est formé par un simple demi-cercle (le point marque l'origine de l'arc de cercle). Cette figure se passe d'explication. En second (fig. 3c), nous trouvons un arc brisé basé sur une ligne séparée en trois parties. Dans la figure la 3d, apparaît le fameux « tiers-point » que je viens d'évoquer. Reliés, les points du tracé forment un triangle équilatéral.

Fig. 3b - Arc plein-cintre

Fig. 3c - Arc brisé
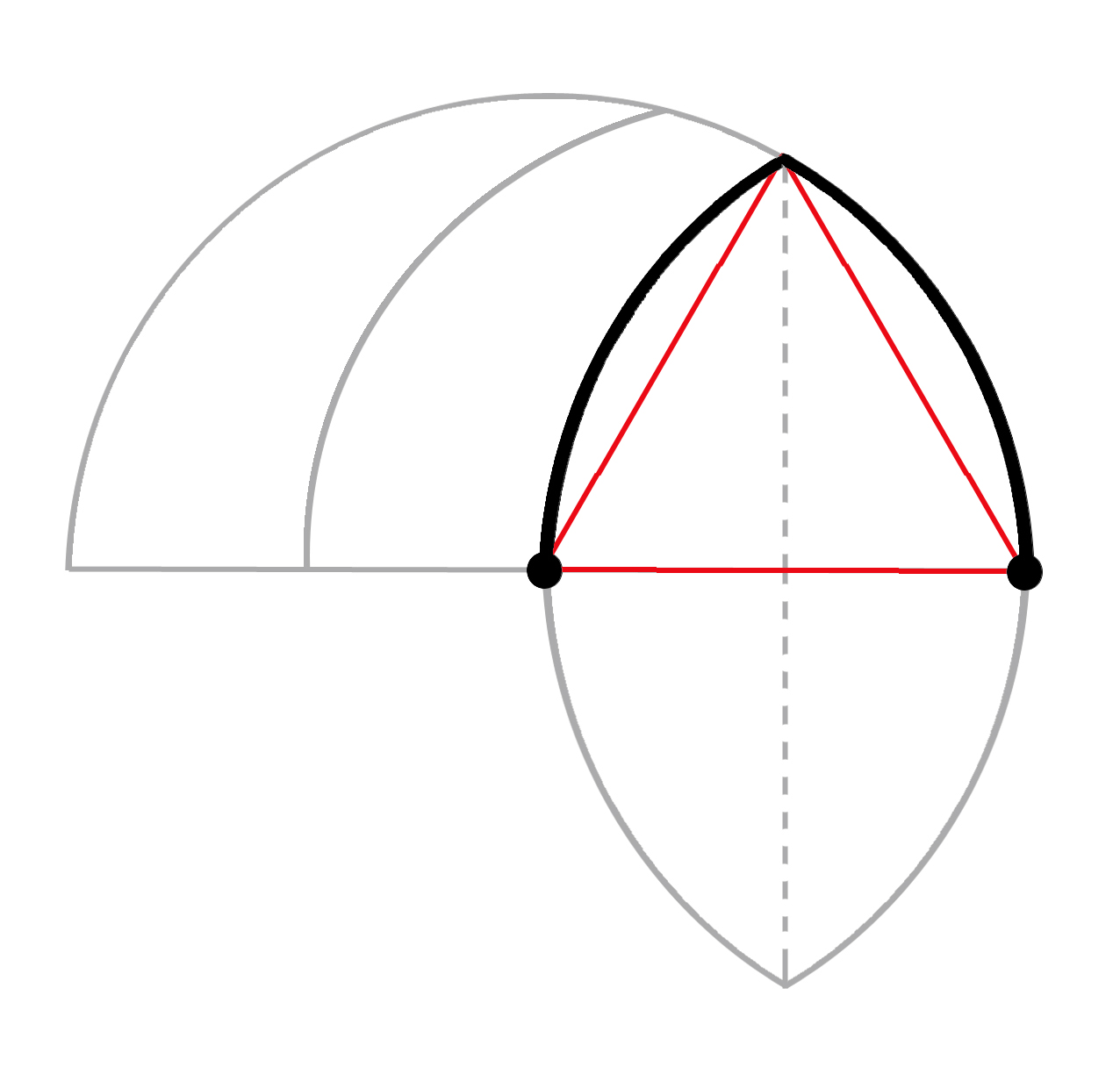
Fig. 3d - Arc en tiers-point
Note : les points marquent les origines des arcs de cercle.
Selon le même principe, la ligne aurait pu être divisée par trois, quatre ou cinq points afin de définir des arcs d'ouvertures différentes. Le lecteur intéressé pourra trouver dans l'annexe géométrie (1), de plus amples informations sur les tracés de voûtes.
Le triangle, comme tous les polygones, donne naissance à un rectangle régulateur c'est-à-dire la forme initiale d'un tracé géométrique, sa nature. Je vais prendre un exemple sur lequel nous reviendrons bientôt, la croisée du transept de la cathédrale de Reims (fig. 4a). Si l'on tire un arc de cercle entre les deux colonnes du bas, on constate que l'arc coupe à la fois l'axe médian vertical et la ligne dessinée par l'arc-doubleau (fig. 4b). Si nous relions ces trois points, nous obtenons un triangle équilatéral (fig. 4c). En dernier lieu, on peut construire autour de ses sommets un rectangle (fig. 4d).

Fig. 4a

Fig. 4b

Fig. 4c

Fig. 4d
Ici nous sommes guidés par le dessin du plan, mais en reproduisant cette construction directement sur une feuille vierge, nous obtiendrions le même résultat, la même proportion. C'est ce que j'appelle retracer.
« Le point se place dans le carré ». De forme stable, le carré est capable d'indiquer les points cardinaux, les quatre éléments, les quatre saisons. Ainsi, la cathédrale s'élève-t-elle sur le carré de la terre, lui-même issu du carré du ciel. Le rapport n'est plus à faire entre cette figure et l'architecture ou il est omniprésent.
Reprenons l'exemple du chapitre précédent consacré à l'analyse d'une nef. Le résultat révélait une construction basée sur la diagonale d'un carré. À la place d'un carré, c'est un triangle que j'aurais pu choisir ou toute autre combinaison entre ces formes (fig. 5). Au final, la réunion de ces figures forme un polygone sur lequel est directement construit l'un des tracés de voûtes que nous venons d'étudier.

Fig. 5 - Élévations construites à base de carrés et de triangles
On remarquera, à droite de la figure 5, le procédé permettant de reporter les deux tiers de la largeur d'une ligne (fig. 6a). C'est une proportion équivalente à celle d'un triangle ou les cathètes feraient respectivement trois et deux unités (fig. 6b).
Maintenant, si l'on double ce report de deux tiers, nous obtenons un côté de 4 sur une base qui reste de 3, soit les proportions du triangle de Pythagore.

Fig. 6a - Report de 2/3 d'une largeur

Fig. 6b - Triangle 3/2 équivalent
Dans la même idée, on comprendra que d'autres triangles peuvent servir à construire un polygone régulateur. Comme on le voit, l'élévation est toujours réglée par des rapports géométriques simples.
Commentaires
La démonstration de Pierre Bellenguez sur la géométrie des cathédrales est absolument remarquable de simplicité et d'efficacité. Elle est très convaincante, et en plus, très élégante, ce qui est bon signe. L'architecte Viollet le Duc avait lui aussi proposé en son temps une hypothèse de géométrie sacrée en étudiant les coupes des cathédrales, mais ses résultats n'étaient pas très probants. Les points de ses figures tombaient un peu n'importe où et l'ensemble manquait de la clarté qui arrive toujours lorsqu'on a découvert le principe directeur d'un dessin. La démonstration de Pierre Bellenguez tient elle bien mieux la route. Elle est donc supérieure à celle de l'immense Viollet le Duc, ce n'est pas rien. Franchement bravo.
David Orbach (Architecte - Ingénieur structure - Enseignant à l’Université Populaire de Caen de Michel Onfray)
JE VOUS CONSEILLE SANS RÉSERVE la lecture du nouvel opus de Pierre Bellenguez, consacré au décryptage des tracés géométriques de la basilique de Vézelay. En seulement quelques dizaines de pages et d'illustrations, sans sombrer un seul instant dans les spéculations zozotériques et en s'appuyant notamment à très bon escient sur un schéma explicite du carnet de Villard de Honnecourt, l'auteur fournit au lecteur des clés immédiatement compréhensibles, limpides, de la compréhension géométrique de l'édifice.
Jean-Michel Mathonière - Directeur éditorial chez Éditions Dervy - Historien des compagnonnages
Au cathédraloscope, nous présentons les travaux de Pierre Bellenguez qui développe le concept de matrice première qui permettre aux bâtisseurs de dresser d'une manière cohérente les plans d'élévation d'une cathédrale. Il démontre dans son livre "les cathédrales retracées" la pertinence de son hypothèse.
Cathédraloscope
Dans son livre, Pierre Bellenguez, passionné d’architecture gothique, décrypte les constructions des bâtisseurs en se mettant dans la peau de ces derniers. A l’aide de différentes cathédrales gothiques françaises, il réfute des théories populaires sur ces édifices et démontre l’usage des figures géométriques dans ces bâtiments. Il s’intéresse également au symbolisme présent au cœur des cathédrales en analysant différents éléments architecturaux et historiques. Son œuvre nous a été particulièrement utile afin d’illustrer les méthodes géométriques des cathédrales gothiques [...]
Site : lescathedrales.wordpress.com
Un ouvrage extraordinaire où l’on ne fait pas de rapport entre la distance de la terre à la lune avec l’hypoténuse de la face de la pyramide en vraie grandeur, mais où les tracés sont opératifs […] car tout commence, quelle que soit l’épure […] en trait carré.
Jean-Pierre Bourcier - Spécialiste du trait
Pierre Bellenguez, déjà auteur d'un ouvrage sur les cathédrales, propose, avec ce livret, de découvrir l'univers de la basilique de Vézelay autrement, en essayant de comprendre comment celle-ci a été bâtie, quels symboles géométriques renferme-t-elle, en étudiant le portail et les symboles représentés. Un volume richement illustré (photos, plans, coupes, élévations) à lire d'urgence !
Olivier Petit - Médiéviste
Le Livre du Jour est : Les cathédrales retracées Les nombres régissent nos grands édifices. Pour bien le comprendre, il faut sortir ses outils de géomètre et chercher les proportions. Un travail méthodique et plein de bon sens dans les nefs, croisées et transepts, dans les absides et les chevets, et bien sûr dans les élévations. Une promenade qui nous conduit à Amiens, Vézelay, Beauvais, Chartres Bourges et Reims … Un bonheur d’ouvrage que nous devons à Pierre Bellenguez
Jean-François Lecompte - écrivain
Je recommande... Le superbe ouvrage Les cathédrales retracées pour tous les passionnés d'architecture gothique. Dans son livre, l'auteur Pierre Bellenguez nous dévoile le message caché derrière les plans des grandes cathédrales gothiques. À consommer sans modération !
Luciano Xavier - Maquettiste en cathédrales gothiques
Dans ce livre, je m'attendait à entendre beaucoup parler de géométrie sacrée, de traditions et de société secrète et bien pas du tout... Pour mon plus grand bonheur et mon plus grand plaisir, c'est un livre précis, sourcé, technique, néanmoins facile d'accès, qui permet à un néophyte d'aborder le sujet sans difficultés. L'auteur est très pédagogue, ça se lit tout seul. [...] Clairement, ce livre va véritablement m'aider pour mon travail sur les mystères des cathédrales. [...] Encore une fois je remercie chaleureusement Pierre Bellenguez pour son livre les cathédrales retracées.
Arcana Les Mystères du Monde - Youtubeur (Chaine Arcana)
Avis de lecteur (Priceminister) Beau et instructif. Ouvrage superbe avec d'abondantes illustrations en noir ou couleurs. Avec une simplicité communicative, l'auteur décrypte la science des bâtisseurs. Il réécrit avec clarté et à l'aide d'abondantes études personnelles les techniques qui ont permis cette révolution dans l'architecture. Loin d'être un remake de littératures courantes, c'est un beau livre à offrir ou à se faire offrir.
troph38
Le Mot du Jour est : « Encore Vézelay »? Un livret abondamment illustré sur la géométrie particulière de Vézelay vient d’être édité par Pierre Bellenguez. Ayant eu le privilège de le lire avant l’impression je vous le recommande, car compas en mains c’est de la belle ouvrage ! Les illustrations sont superbes et pédagogiques, alors, comme en plus c’est pas cher (15€), que ça s’achète en ligne et que ça tiendra dans le sac de plage, offrez-le-vous au plus vite !
Jean-François Lecompte - écrivain
J'ai lu votre livre d'une traite et vais bientôt le relire plus lentement. Merci et bravo, vous avez répondu à tellement de mes questions.
John Brown
Formidable ouvrage technique touffu mais très intéressant pour qui s’intéresse à cette magnifique architecture et à l’art des bâtisseurs... Merci Monsieur
Armand Priest (ESTP) - Commentaire Facebook
Pierre Bellenguez explique très bien le sens de la géométrie des cathédrales en prenant appui sur la basilique de Vézelay, dans son ouvrage [...] Les cathédrales retracées : la science des bâtisseurs
Anthony CRESTIN - La géométrie et le mythe
Passionné d'architecture, Pierre Bellenguez a repris les mesures des cathédrales et compris comment les bâtisseur ont réussi ces exploits architecturaux. Aucun nombre magique, mais du bon sens, de la simplicité et de l'expérience.
Joël Supéry - Site tuskaland.com
Regard d'un passionné d'architecture médiévale sur l'architecture secrète des cathédrales et la géométrie gothique. Un ouvrage très utile pour notre projet #STEAMBuilders (https://steambuilders.eu/fr/) qui a pour objectif de fournir aux enseignants des outils et la pédagogie nécessaires à la mise en œuvre de l'approche innovante et pluridisciplinaire des STEAM par la manipulation et la reconstruction de techniques et de patrimoine historiques !
Asso Fermat-Science
J'ai bien reçu votre admirable livre "Les cathédrales retracées" et je vous en remercie. Étant passionné par l'architecture sacrée j'ai pu l'apprécier. Encore merci. Cordialement,
M. Moldovan
"Dans le sillage du livre "Les cathédrales retracées", Pierre Bellenguez nous entraîne dans une visite initiatique de la basilique de Vézelay, à la découverte des procédés géométriques utilisés par les moines bâtisseurs. Compas en main, il nous fait découvrir l’alphabet de ce livre de pierre, la fascinante science des anciens maîtres d’œuvre". La basilique de Vézelay, un incontournable... !
Catherine Leschenne








Après son magnifique ouvrage intitulé : " Les cathédrales retracées ", je vous recommande vivement de découvrir le nouvel opus de l'excellent Bellenguez Pierre, consacré au décryptage des tracés géométriques de la basilique de Vézelay.
Dominique Gury