Gothic and the golden ratio

      Speculative geometry has its games, its uselessness, like the other sciences.

Châteaubriant

On the previous page, I invalidated the relevance of mathematics alone in the analysis of Gothic tracings. Logically, this approach excludes the use of the golden ratio. Indeed, if the golden ratio can be expressed geometrically, the fact remains that its interpretation, the very idea of its singularity as an irrational number, places it squarely in the lap of mathematics. Isn't it universally accepted that the golden ratio governs the layout of cathedrals?

Let's start with a reminder for those unfamiliar with this relationship. It is represented by the Greek letter Phi, symbol ?. Its numerical value, 1.618, offers some curious mathematical properties:

? - 1 = 0.618
1/ ? = 0.618
? = 1.618
? + 1 = 2.618
? / 0.618 = 2.618
? x ? = 2.618
0.2618*12 = 3.1416   

This ratio can be obtained using very simple geometric layouts. For example, as shown in Fig. 1, we need only determine half the base of a square, i.e. point M, in order to draw a circular arc of radius MD that intersects the extension of the line at C.
The ratio between segments AB and AC gives ?, the golden ratio. The rectangle we've just formed expresses a golden rectangle, as does the figure as a whole. In a few lines, we'll see the same pattern again.

.
Fig. 1 - Geometric construction of the golden ratio

The golden ratio is put to all sorts of uses. It's supposed to provide the most beautiful aesthetic proportion, regulate the growth of our genes or direct the dimensions of the Khéops pyramid. Nothing less.

But what's the historical background? It is often claimed that Pythagoras held the secret. This is to forget that the golden ratio is an irrational number. Limited to integers, Pythagoras abhorred them. They challenged his geometric interpretation of the world, in which every number is a length. Even if they existed, nobody was supposed to know about them. Legend has it that his disciple, Hippasius of Metapontum, was drowned simply for talking about it. In any case, between knowing about the existence of a thing and understanding it mathematically, there was a step that Greek knowledge could not take.
So why invoke Pythagoras against all historical plausibility? The reason probably lies in the Pythagorean school's decision to use a pentagon as a sign of recognition. The reasoning is simple: the geometry of the pentagon expresses the golden ratio; therefore, Pythagoras knew the golden ratio! It's a perfect example of paralogism, or even sophistry in the arguments of some...

Euclid later noted this relationship "in extreme and average reason", without measuring its significance. He would have had to be able to calculate its algebraic value, something that the time was incapable of doing. A translation of Euclid by the geometrician monk Campanus from Novara was produced in the _13th century, but his commentaries were not published until 1409. The Gothic era had come to an end.
Much later, in the early _16th century, the monk Lucas Pacioli di Borgo studied Euclid in his De divina proportione. For him, this geometric proportion proves the existence of God. This was the genesis of the famous "Divine Proportion".
In the _19th century, it was the turn of the German philosopher Adolf Zeising to take an interest in this relationship. He called it the "golden section". For him, it was an aesthetic system that he sought to discern in all fields, including biology and architecture.
But the modern infatuation with this number owes everything to Prince Matila Costiesco Ghyka, author of the indispensable Le nombre d'or. For those who refer to it, it forms an aesthetic proportion, a mathematical message that presides over all ancient artistic and architectural conceptions.

However, the only thing I'm interested in here is whether medieval builders used the golden ratio, because it's a given that they didn't.
To verify this, I've studied dozens of monuments, following the example of M. Labouret(whose work I highly recommend you read). For example, the transept of Strasbourg Cathedral is supposed to have the same ratio of external length to internal width. Here's where the problem lies: "Too bad if one of the two figures includes the thickness of the walls and buttresses and the other doesn't."
And, on this point, I can only agree with him. You can't establish a relationship between a benchmark located inside a structure and one located outside. This is a gross methodological error, to which I shall return later.

Let's take a look at Dol-de-Bretagne cathedral. It is often presented as having a plan governed by golden rectangles. Several studies have been devoted to it. In this study, a geometric construction has been superimposed on the plan of the building. It consists of four squares, two of which overlap at the level of the transept, which is central here (fig. 2).

 
.
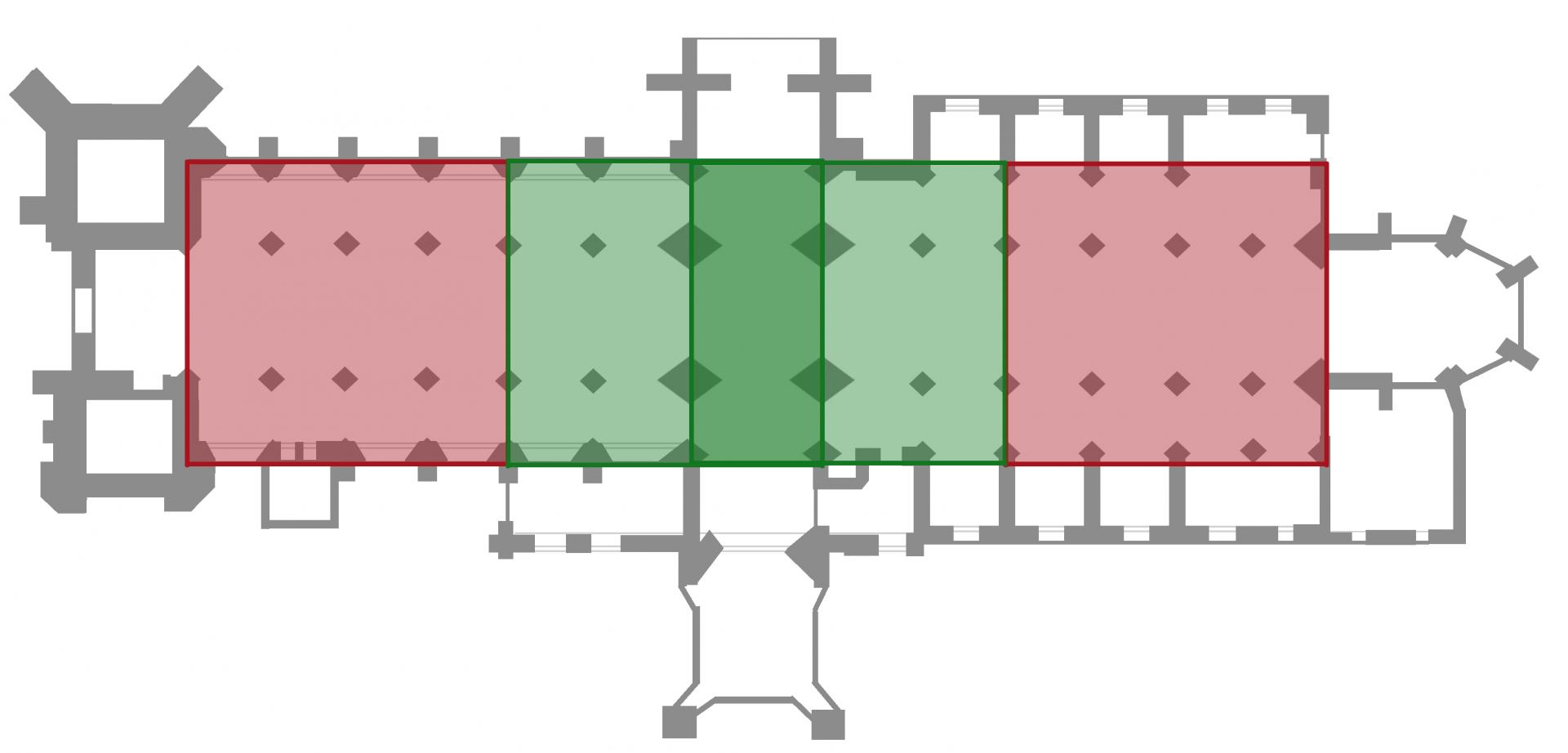
Fig. 2 - The four supposed squares

Now, if we cut the overlapping squares by the transept lines, we can obtain three rectangles containing a golden ratio (two are formed by the union of the pink and light-green polygons, the last by the two central squares). The whole is equivalent to two symmetrical tracings of a golden rectangle (like the one in fig. 1), each in a double square (fig. 3). Now, if we merge the unused spaces of the long squares, we obtain the surface of the transept and the floor plan of the building.
This is all very elegant, and you'd be forgiven for thinking that the golden ratio governs the spaces of this cathedral. There are, however, a number of awkward points in this theory.
First and foremost, the plan used. Here, I've roughly redrawn it to improve legibility, but the original(see the study) seems to be of dubious quality. This is a recurring problem, which I'll discuss in a few pages.
Cause or consequence, the squares posed as premises are not. They are distorted and not exactly the same size. We'd need a good-quality survey to go any further.
The second point is the absence of a frame of reference, of a working methodology. While the vertical lines of the polygons follow the centers of the pillars, the horizontal lines are aligned with the outer wall on the left and with the outside of the pillars on the right. This is illogical and unacceptable. The proposed layout is therefore different from what it should be. As a result, the squares that weren't squares in the first place aren't squares at all, and the golden proportions are lost.

.
Fig. 3 - The two symmetrical golden lines

The same applies to my attempt to retrace figure 3, which, based on the study's proportions, is totally misleading. To the layman, the demonstration may seem credible, but architecturally and mathematically speaking, it's simply wrong.
Matila Ghyka would not have been moved by these inconsistencies. He invoked the "trembling", the "groping of the living", to justify the discrepancy between his constructions and the plans.

The same applies to the most emblematic cathedral of the Gothic style, Notre-Dame de Paris. Here, the golden ratio is supposed to appear in the proportions of the façade. If you divide the length of the façade (approx. 69 m) by its width (approx. 40 m), you get the Golden Ratio (approx. 1.618) (normally, with the given dimensions, you'd get 1.725, but you'll notice that this result is quite close to the Golden Ratio). Note that the height must include the embellishments on the roof of the towers). We can conclude that the façade was built according to the rules of the Golden Number."
Note the obligation to take into account the "embellishments" and the many "surroundings", which make any calculation impossible. It is therefore impossible to judge the delta between the expected result and the actual result.

Let's overlook the fact that the construction used exceeds the cathedral's footprint, and that in the end, there's no correspondence with an architect's plan. The inconvenient point is that it was impossible for me to obtain anything other than an approximate result with this method. And let's not forget that even an exact explanation would solve nothing, explain nothing. What about the interior proportions, the construction of the transept, the rhythms of the bays or the design of the chevet? It's curious that a talented journeyman carpenter, a specialist in war machines in the Middle Ages, should propose a speculative layout instead of seeking an operative solution in keeping with medieval tradition.

The same applies to the Cistercian abbey of Le Thoronet, and here I quote M. Labouret: "If we stretch the dimensions a little, we interpret the basic module as almost a golden rectangle. And a certain number of geometrical figures, which do not even correspond to the structural points of the monument, are placed on the real plans in order to deduce dimensions corresponding to what we want to demonstrate..."

This is the crux of the problem. The frontispiece to Plato's Academy reads: "No one enters here who is not a geometer". Geometry and architecture are sciences, and as such require a minimum of knowledge and rigor, qualities that many people clearly believe, wrongly, they possess.
George Jouven, chief architect of historic monuments and an undisputed specialist in arithmology, talks about the golden ratio in the _13th century. Whatever Villard de Honnecourt's drawings might lead us to believe," he says, "the Middle Ages had forgotten it. Viollet-le-Duc himself, in his chapter on proportions, says nothing about it. Clearly, the man behind the cathedrals never came across this relationship, nor did Vitruvius or any other architect.

Let me make it clear that my purpose here is not to wage war on the golden ratio - quite the contrary. My only question is whether it was known in the Gothic period. According to my research, the answer is clearly negative. However, some researchers may have been misled. There are constructions that are graphically very close to ?. A ratio of 5/8 gives 0.625, while that of 3/5 gives 0.6. These differences are almost negligible from an operative point of view.
Furthermore, we'll see later that some plans are organized on a double square, the long square, whose diagonal is the square root of five. Now, this irrational number (2.236) is nothing less than the addition of 1.618 + 0.618, i.e. ? + 1/?. Clearly, the use of simple squares is not a deliberate expression of the golden ratio.If we look for it compulsively, it may also emerge from a pentagon or one of the many shapes that potentially contain it. But these are marginal results. Clearly, the golden ratio is not intended to govern a Gothic plan.

As Canon Charles J. Ledit wrote: "It will always be possible to establish relationships (golden or otherwise) between any two points on the monument. A billiard ball, moved by an indefinite energy, will always end up (thanks to the cushions) touching the other two balls. If you draw enough lines between points on a plane, you'll always get some indication (convincing or not)". The myth of the golden ratio being used to direct the layout of Gothic cathedrals clearly needs to be exposed.

N.B. The appendix of the book contains additional information on Gothic proportions and the Golden Ratio, including a rebuttal of Professor Murray's analysis of Amiens Cathedral.