Gothic chevets

      Then I saw the Pendulum. The sphere, movable at the end of a long wire attached to the choir vault, described its ample oscillations with isochronous majesty.

Umberto Eco (Foucault's Pendulum)

It's interesting to study the construction of the polygons that form the apses. On many monuments, you'll notice that the diagonal of the last bay of the choir directly prepares the angle of the polygon. By design, by the choice of an initial proportion, the final layout is anticipated. For those in doubt, note that Villard de Honnecourt drew these lines with the same pencil stroke (Fig. 1),

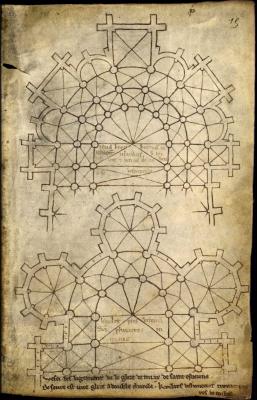
Fig. 1 - Chevet plans (Villard de Honnecourt - folio 29) D.P.

 
I've developed a number of procedures for tracing this type of cut. Here's a particularly interesting one (fig. 2). On the last bay of the choir, a square is formed, the diagonal of which is equal to half the width of the main nave (as shown by the dotted arc).

The height of this square is used to mark the boundary of the apse. At the upper ends of the rectangle thus formed, I mark the pillars, and trace the semicircle of the apse with center O. From the lower corners, I draw two lines that intersect at O, defining two further pillars and cutting the circle.
The distance between the pillars we've just defined determines two of the sides we're looking for. All we need to do is transfer them symmetrically to complete the circle's partition.

Fig. 2 - Partition of an apse into five parts

The technique described above is used for the last bay of the choir and the chevet of many Gothic buildings. It can be found in Reims, the Abbey of Saint-Martin-aux-Bois and the Royal Collegiate Church of Saint-Quentin.

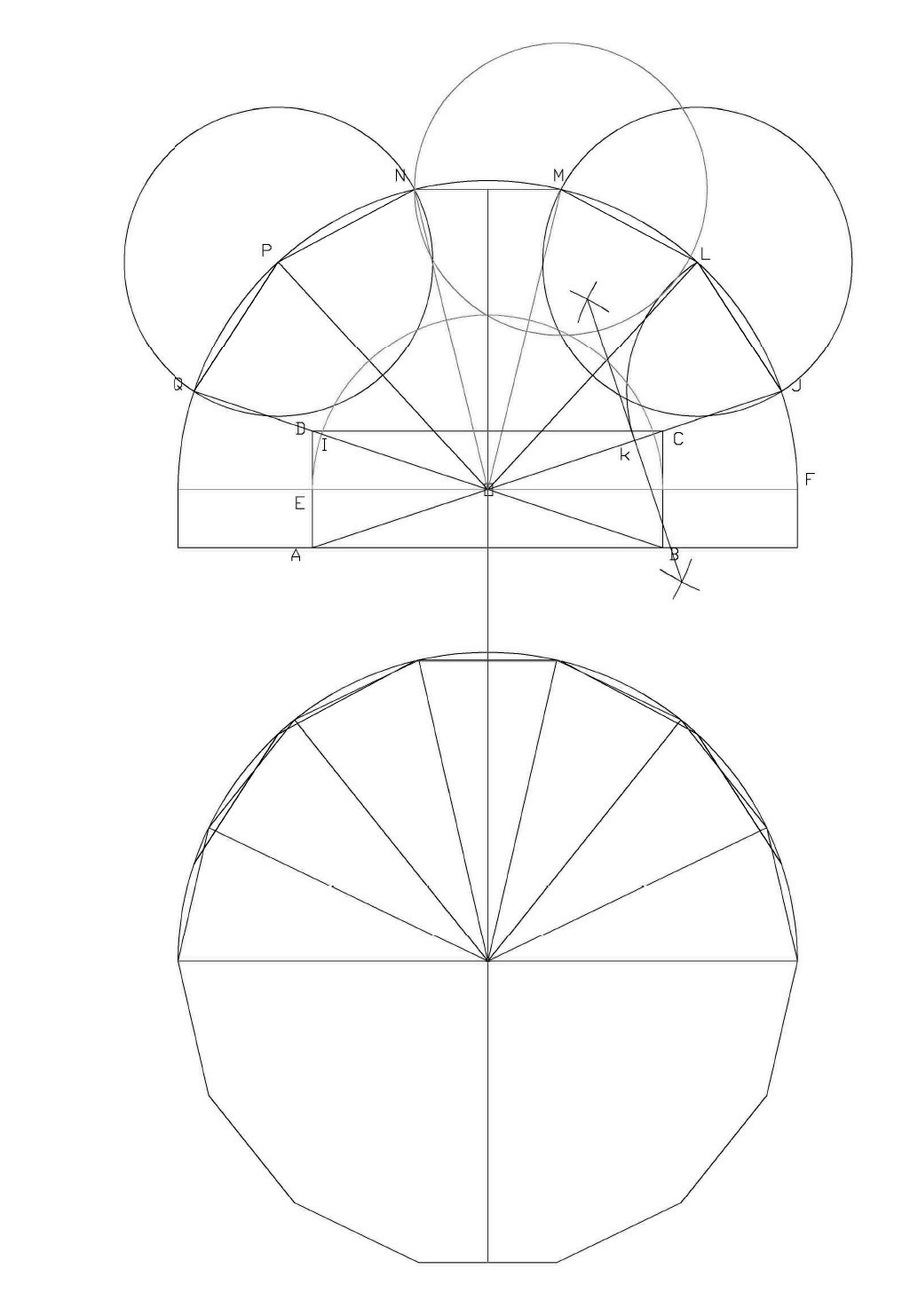
The construction of the chevets crowned by seven chapels (fig. 3) is similar. The width of the central nave is divided into three parts, creating a three-by-one rectangle inside the apse. The intersection of the diagonals (point O) will provide the origin of the circles, while their extensions will create the starting angle and fix the position of the columns.

Fig. 3 - Partition of an apse into seven parts

Knowing that half the length of the straight line is equal to the value to be transferred to the circle to form the angles, it's easy to draw the pseudo heptagon. These are, in fact, one-by-two triangles, arranged in a fan-shape. The process is used in Beauvais and Amiens, among others.
These two chevet constructions are generic systems. It should be noted that some cathedrals, such as Chartres, have their own specific layouts.

The abbey church of Saint-Martin-aux-Bois in the Oise region of France will help illustrate this point (fig. 4). The building features a transeptless aisle, enclosed by an apse similar to that of Reims.
 

Fig. 4 - Choir of Saint-Martin-aux-Bois

We've just seen that the side of the square determines the width of the last bay, while its diagonal is half the length of that same bay. To plot the height of the nave bays, the architect simply used this half-width to form equilateral triangles. There are two such triangles per bay. This segment (the red lines) is common to the entire building. It alone explains the eurhythmics.

In this example, it's hard to tell where the layout of the choir and nave begins. Here, they are of the same nature. You can see a laser scan of this building atsaint-martin-aux-bois.org