
Les chevets gothiques
C'est alors que je vis le Pendule. La sphère, mobile à l'extrémité d'un long fil fixé à la voûte du chœur, décrivait ses amples oscillations avec une isochrone majesté.
Umberto Eco (Le Pendule de Foucault)
Il est intéressant d'étudier la construction des polygones qui forment les absides. Sur de nombreux monuments, vous remarquerez que la diagonale de la dernière travée du chœur prépare directement l’angle du polygone. De par sa conception, de par le choix d’une proportion initiale, le tracé final est anticipé. Pour ceux qui auraient un doute, ils remarqueront que Villard de Honnecourt dessinait ces lignes d'un même coup de crayon (Fig. 1),
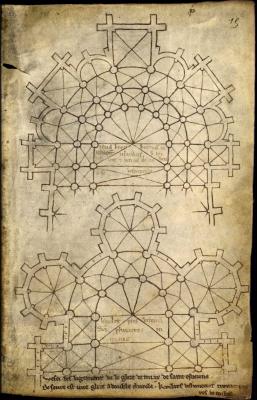
Fig. 1 – Plans de chevets (Villard de Honnecourt - folio 29) D.P.
J'ai développé divers procédés permettant de tracer ce type de découpage. En voici un particulièrement intéressant (fig. 2). Sur la dernière travée du chœur, on détermine un carré dont la diagonale est égale à la demi-largeur du vaisseau principal (ce que met en évidence l’arc de cercle dessiné en pointillés).
La hauteur de ce carré permet de tracer la limite de l’abside. Aux extrémités supérieures du rectangle ainsi formé, je marque les piliers, et trace le demi-cercle de l’abside de centre O. Des coins inférieurs, il restera à tirer deux lignes qui se croiseront en O, et définiront deux autres piliers en coupant le cercle.
L’écart entre les piliers que nous venons de définir, déterminent deux des côtés recherchés. Il suffira donc de les reporter symétriquement pour finaliser la partition du cercle.

Fig. 2 – Partition d’une abside en cinq parties
Le procédé que nous venons de voir dirige la dernière travée du chœur et le chevet de nombreux bâtiments gothiques. On le retrouve aussi bien à Reims, qu’à l’abbaye de Saint-Martin-aux-Bois ou à la collégiale royale de Saint-Quentin.
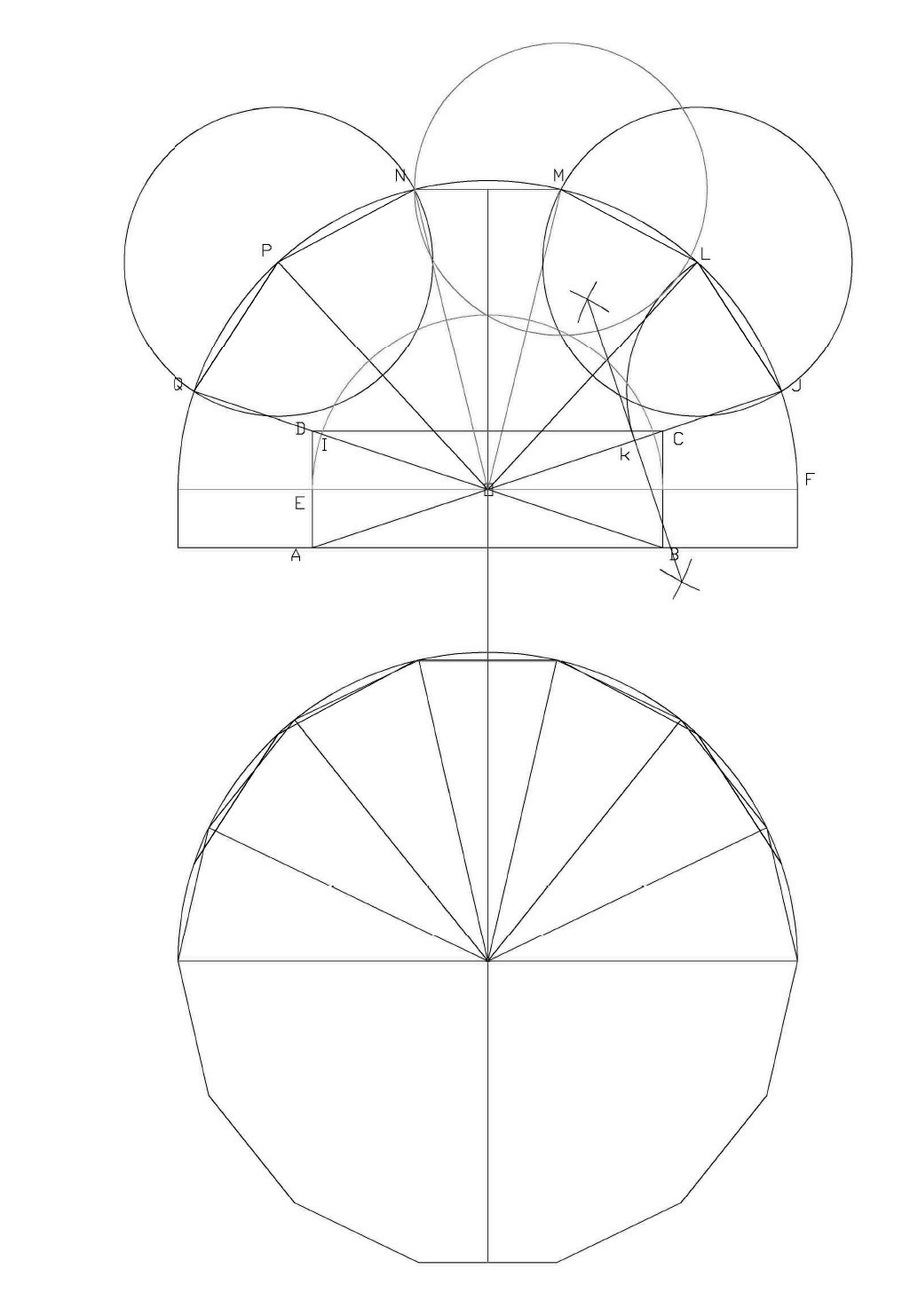
Quant aux chevets couronnés par sept chapelles (fig. 3) leur construction est de la même eau. La largeur du vaisseau central est divisée en trois parties, ce qui permet de dessiner un rectangle de trois sur un à l’intérieur de l’abside. L’intersection des diagonales (point O) va fournir l’origine des cercles, alors que leurs prolongements vont créer l’angle de départ et fixer la position des colonnes.

Fig. 3 – Partition d’une abside en sept parties
Sachant que la moitié de la longueur de la droite est égale à la valeur qu’il faudra reporter sur le cercle pour former les angles, rien n’est plus simple que de tracer le pseudo heptagone. Ce sont en fait, des triangles d’un sur deux, disposés en éventail. Le procédé se retrouve entre autres à Beauvais ou Amiens.
Ces deux constructions de chevets sont des systèmes génériques. A noter que certaines cathédrales ont des tracés qui leurs sont propres, comme par exemple Chartres.
L’abbatiale Saint-Martin-aux-Bois dans l’Oise va me permettre d’illustrer ce discours (fig. 4). Le bâtiment propose une allée sans transept, clôturée par une abside similaire à celle de Reims.

Fig. 4 - Chœur de Saint-Martin-aux-Bois
Nous venons de voir que le côté du carré détermine la largeur de la dernière travée, alors que sa diagonale équivaut à la demi-longueur de cette même travée. Pour tracer la hauteur des travées de la nef, l’architecte a simplement utilisé cette demi-largeur pour former des triangles équilatéraux. On en retrouve donc deux par travée. Ce segment (les lignes rouges) est commun à tout l’édifice. À lui seul, il en explique l’eurythmie.
Dans cet exemple, on à du mal à savoir ou commence le tracé du chœur et celui de la nef. Ici, ils participent d'une même nature. Vous pouvez découvrir la scannographie laser de cet édifice sur le site saint-martin-aux-bois.org
Tracés des absides de l’abbaye du Mont Saint-Michel et de Notre-Dame d’Évreux
Dans le reportage "Mont-Saint-Michel - Le labyrinthe de l'archange" à 1h 15' 52'' , le professeur d'histoire d'art médiéval Yves Gallet, met en évidence une correspondance de proportions entre le chevet de cette abbaye et celui de la cathédrale d'Évreux. Il constate également que des piles du chœur sont chemisées sur des supports romans, tout comme les colonnes de la crypte. On comprendra que l'architecte a été contraint de suivre un rythme roman préexistant.
Une question se pose alors, le tracé du chevet de la cathédrale de Troyes étant similaire à celui du Mont, ne serait-il pas lui-même le reflet d'un procédé roman ? L'histoire de Notre-Dame d'Évreux semble infirmer cette hypothèse. D'après Philippe Gavet, l'ancienne cathédrale romane d'Évreux se rapprocherait de l'Abbatiale de la Trinité de Caen, laquelle arbore un chevet segmenté en cinq parties et non pas en sept. Toutefois cet élément ne peut à lui seul balayer l'hypothèse.
Au niveau du tracé géométrique, la segmentation des chevets d'Évreux et du Mont est la plus simple qui se puisse imaginer. La largeur de la nef est divisée en sept parties, sept unités. À une unité d'écart est posé le demi-cercle du chœur. À partir d'une des limites de ce même chœur, seront ensuite tracés, un arc d'un rayon de deux unités, un arc égal à la demi-largeur de la nef, ainsi qu'un arc égal à cinq unités. En coupant le demi-cercle, ces arcs déterminent les centres exacts des piles.
Comme on peut l'imaginer, la segmentation obtenue par ce procédé n'est pas régulière, mais on constate exactement les mêmes écarts sur les plans.

Spécialiste du trait technique et de la stéréotomie, Monsieur Jean Pierre Bourcier a contrôlé mes démonstrations géométriques d'un point de vue numérique. Je vous livre ici ses analyses et avis sur les tracés que nous venons de voir.
Analyse du tracé de la figure 2 (réalisé sous AutoCAD)
« Soit (A,B) la largeur de la nef et (U,V) son axe. Du point B tracer (B,M) tel que l'angle (A,B,M) est égal à 45°. Tracer l'arc de cercle de rayon (B,U) de centre B. Il coupe (B,M) en I. De I tracer la ligne (D,C) parallèle à (A,B). Cette droite trace la limite du chœur.
Soit O milieu de (D,C) tracer la droite (O,B). Elle coupe le demi-cercle de rayon (O ,D) en P, qui est le centre de la deuxième pile, D étant la position de la première pile. Pour tracer le centre des autres piles, il suffit de reporter en (P ,Q) puis (Q,R) la corde (D,P). On constate alors que la corde QT est plus grande que la corde DP.
Si on conserve le point P et son symétrique W comme référence, le point Q et son symétrique T définis par report de la corde (D,P), alors la corde (Q,T ) est supérieure aux quatre autres.
Soit DP=CW=WT=PQ avec QT > DP, ce qui donne pour une nef de 12 m de large DP =3634.87 QT=4000 alors que le coté du décagone inscrit au cercle de rayon OD est de 3708.3
Si on considère le point T, l'écart entre ce tracé et le tracé du décagone théorique est de 145.33 mm suivant un axe perpendiculaire à l'axe de la nef et de 49.48 mm suivant un axe parallèle à l'axe de la nef, le centre de la pile restant sur le cercle de rayon OD, en regard de la fonction de la pile et des instruments de mesure utilisés à l'époque, l'écart est tout à fait acceptable. »

Analyse du tracé de la figure 3 :
« Soit AB la largeur de la nef et UV son axe AB est divisé en trois parties égales. Le rectangle ABCD de petit côté AB/3 est tracé. Les deux diagonales sont tracées leurs intersections le point O est le centre des axes circulaires des piles. Ce point O est aussi le point de concours des axes rayonnant des piles.
Soit le cercle de rayon OE le centre de la première pile sera son point d'intersection I avec la diagonale OD.
Soit à tracer le centre des piles situées sur le cercle de rayon OF. La diagonale OC est prolongée sont intersection avec le cercle de rayon OF défini le centre de la première pile en J.
Soit K le milieu de OJ, le segment JK est la corde a reporter sur le cercle de rayon OF pour obtenir les points L et M centre des deux piles suivantes JL= JK LM = OJ/2.
Par symétrie par rapport à l'axe de la nef on définit les points N P et Q centres des piles suivantes. L'intersection des droites rayonnantes en O et passant par les entres des piles du cercle de rayon OF avec le cercle de rayon OE définit les centres des piles appartenant à ce cercle.
On constate alors que JL=LM =NP =PQ avec MN < JL, ce qui donne pour une nef de 12 m de large et OF = 10616 (valeur quelconque) JL=5308 MN=5012.34 le coté du polygone régulier à 14 cotés inscrit au cercle de rayon 0F étant de 4724.56
Si on considère le point M, l'écart entre ce tracé et le tracé du polygone régulier à 14 cotés inscrit au cercle de rayon OF est de 143.9 mm suivant un axe perpendiculaire à l'axe de la nef et de 33.9 mm suivant un axe parallèle à l'axe de la nef, le centre de la pile restant sur le cercle de rayon OF en regard de la fonction de la pile et des instruments de mesure utilisés à l'époque, cela est tout à fait acceptable. »
Commentaires
La démonstration de Pierre Bellenguez sur la géométrie des cathédrales est absolument remarquable de simplicité et d'efficacité. Elle est très convaincante, et en plus, très élégante, ce qui est bon signe. L'architecte Viollet le Duc avait lui aussi proposé en son temps une hypothèse de géométrie sacrée en étudiant les coupes des cathédrales, mais ses résultats n'étaient pas très probants. Les points de ses figures tombaient un peu n'importe où et l'ensemble manquait de la clarté qui arrive toujours lorsqu'on a découvert le principe directeur d'un dessin. La démonstration de Pierre Bellenguez tient elle bien mieux la route. Elle est donc supérieure à celle de l'immense Viollet le Duc, ce n'est pas rien. Franchement bravo.
David Orbach (Architecte - Ingénieur structure - Enseignant à l’Université Populaire de Caen de Michel Onfray)
JE VOUS CONSEILLE SANS RÉSERVE la lecture du nouvel opus de Pierre Bellenguez, consacré au décryptage des tracés géométriques de la basilique de Vézelay. En seulement quelques dizaines de pages et d'illustrations, sans sombrer un seul instant dans les spéculations zozotériques et en s'appuyant notamment à très bon escient sur un schéma explicite du carnet de Villard de Honnecourt, l'auteur fournit au lecteur des clés immédiatement compréhensibles, limpides, de la compréhension géométrique de l'édifice.
Jean-Michel Mathonière - Directeur éditorial chez Éditions Dervy - Historien des compagnonnages
Au cathédraloscope, nous présentons les travaux de Pierre Bellenguez qui développe le concept de matrice première qui permettre aux bâtisseurs de dresser d'une manière cohérente les plans d'élévation d'une cathédrale. Il démontre dans son livre "les cathédrales retracées" la pertinence de son hypothèse.
Cathédraloscope
Dans son livre, Pierre Bellenguez, passionné d’architecture gothique, décrypte les constructions des bâtisseurs en se mettant dans la peau de ces derniers. A l’aide de différentes cathédrales gothiques françaises, il réfute des théories populaires sur ces édifices et démontre l’usage des figures géométriques dans ces bâtiments. Il s’intéresse également au symbolisme présent au cœur des cathédrales en analysant différents éléments architecturaux et historiques. Son œuvre nous a été particulièrement utile afin d’illustrer les méthodes géométriques des cathédrales gothiques [...]
Site : lescathedrales.wordpress.com
Un ouvrage extraordinaire où l’on ne fait pas de rapport entre la distance de la terre à la lune avec l’hypoténuse de la face de la pyramide en vraie grandeur, mais où les tracés sont opératifs […] car tout commence, quelle que soit l’épure […] en trait carré.
Jean-Pierre Bourcier - Spécialiste du trait
Pierre Bellenguez, déjà auteur d'un ouvrage sur les cathédrales, propose, avec ce livret, de découvrir l'univers de la basilique de Vézelay autrement, en essayant de comprendre comment celle-ci a été bâtie, quels symboles géométriques renferme-t-elle, en étudiant le portail et les symboles représentés. Un volume richement illustré (photos, plans, coupes, élévations) à lire d'urgence !
Olivier Petit - Médiéviste
Le Livre du Jour est : Les cathédrales retracées Les nombres régissent nos grands édifices. Pour bien le comprendre, il faut sortir ses outils de géomètre et chercher les proportions. Un travail méthodique et plein de bon sens dans les nefs, croisées et transepts, dans les absides et les chevets, et bien sûr dans les élévations. Une promenade qui nous conduit à Amiens, Vézelay, Beauvais, Chartres Bourges et Reims … Un bonheur d’ouvrage que nous devons à Pierre Bellenguez
Jean-François Lecompte - écrivain
Je recommande... Le superbe ouvrage Les cathédrales retracées pour tous les passionnés d'architecture gothique. Dans son livre, l'auteur Pierre Bellenguez nous dévoile le message caché derrière les plans des grandes cathédrales gothiques. À consommer sans modération !
Luciano Xavier - Maquettiste en cathédrales gothiques
Dans ce livre, je m'attendait à entendre beaucoup parler de géométrie sacrée, de traditions et de société secrète et bien pas du tout... Pour mon plus grand bonheur et mon plus grand plaisir, c'est un livre précis, sourcé, technique, néanmoins facile d'accès, qui permet à un néophyte d'aborder le sujet sans difficultés. L'auteur est très pédagogue, ça se lit tout seul. [...] Clairement, ce livre va véritablement m'aider pour mon travail sur les mystères des cathédrales. [...] Encore une fois je remercie chaleureusement Pierre Bellenguez pour son livre les cathédrales retracées.
Arcana Les Mystères du Monde - Youtubeur (Chaine Arcana)
Avis de lecteur (Priceminister) Beau et instructif. Ouvrage superbe avec d'abondantes illustrations en noir ou couleurs. Avec une simplicité communicative, l'auteur décrypte la science des bâtisseurs. Il réécrit avec clarté et à l'aide d'abondantes études personnelles les techniques qui ont permis cette révolution dans l'architecture. Loin d'être un remake de littératures courantes, c'est un beau livre à offrir ou à se faire offrir.
troph38
Le Mot du Jour est : « Encore Vézelay »? Un livret abondamment illustré sur la géométrie particulière de Vézelay vient d’être édité par Pierre Bellenguez. Ayant eu le privilège de le lire avant l’impression je vous le recommande, car compas en mains c’est de la belle ouvrage ! Les illustrations sont superbes et pédagogiques, alors, comme en plus c’est pas cher (15€), que ça s’achète en ligne et que ça tiendra dans le sac de plage, offrez-le-vous au plus vite !
Jean-François Lecompte - écrivain
J'ai lu votre livre d'une traite et vais bientôt le relire plus lentement. Merci et bravo, vous avez répondu à tellement de mes questions.
John Brown
Formidable ouvrage technique touffu mais très intéressant pour qui s’intéresse à cette magnifique architecture et à l’art des bâtisseurs... Merci Monsieur
Armand Priest (ESTP) - Commentaire Facebook
Pierre Bellenguez explique très bien le sens de la géométrie des cathédrales en prenant appui sur la basilique de Vézelay, dans son ouvrage [...] Les cathédrales retracées : la science des bâtisseurs
Anthony CRESTIN - La géométrie et le mythe
Passionné d'architecture, Pierre Bellenguez a repris les mesures des cathédrales et compris comment les bâtisseur ont réussi ces exploits architecturaux. Aucun nombre magique, mais du bon sens, de la simplicité et de l'expérience.
Joël Supéry - Site tuskaland.com
Regard d'un passionné d'architecture médiévale sur l'architecture secrète des cathédrales et la géométrie gothique. Un ouvrage très utile pour notre projet #STEAMBuilders (https://steambuilders.eu/fr/) qui a pour objectif de fournir aux enseignants des outils et la pédagogie nécessaires à la mise en œuvre de l'approche innovante et pluridisciplinaire des STEAM par la manipulation et la reconstruction de techniques et de patrimoine historiques !
Asso Fermat-Science
J'ai bien reçu votre admirable livre "Les cathédrales retracées" et je vous en remercie. Étant passionné par l'architecture sacrée j'ai pu l'apprécier. Encore merci. Cordialement,
M. Moldovan
"Dans le sillage du livre "Les cathédrales retracées", Pierre Bellenguez nous entraîne dans une visite initiatique de la basilique de Vézelay, à la découverte des procédés géométriques utilisés par les moines bâtisseurs. Compas en main, il nous fait découvrir l’alphabet de ce livre de pierre, la fascinante science des anciens maîtres d’œuvre". La basilique de Vézelay, un incontournable... !
Catherine Leschenne








Après son magnifique ouvrage intitulé : " Les cathédrales retracées ", je vous recommande vivement de découvrir le nouvel opus de l'excellent Bellenguez Pierre, consacré au décryptage des tracés géométriques de la basilique de Vézelay.
Dominique Gury