

L'étude suivante a été effectuée par J.P. Bourcier après lecture du livre Les clés de Vézelay. L'intention est de vérifier la vraisemblance des tracés proposés. Contrairement à l'enchainement donné dans le livre, qui fait naitre la croisée gothique à partir de la nef romane préexistante, Mr Bourcier effectue cette construction à rebours, c'est-à-dire de la croisée vers la nef. Cette démarche permet d'inverser le sens des progressions géométriques et donc de mettre en évidence d'éventuels écarts.
Pour ceux qui n'ont pas lu le livre, je me dois de donner une explication sans laquelle l'exercice suivant resterait obscur. La nef de Vézelay a été construite bien avant la croisée du transept. Elle présente 10 travées géométriquement formées par des triangles équilatéraux placés tête-bêche.

Pour sa part, la croisée est constituée de deux carrés accolés à deux triangles équilatéraux. En effet, dans les édifices gothiques, la croisée prend fréquemment la forme d’un triangle équilatéral, alors que les croisées romanes privilégient la forme carrée. Sachant que ces deux types d’architectures coexistent dans la basilique, on comprend que la partie supérieure de la Table (basée sur des triangles) a été conçue pour régir l’ensemble gothique, alors que la partie inférieure (basée sur des carrés) était chargée de prendre en compte la nef romane.
Ainsi, le segment rouge que vous pouvez observer sur la planche de droite permet de prendre en compte les proportions des travées de la nef. La longueur qu’il détermine est strictement identique aux côtés des triangles des travées, soit leurs largeurs respectives. Grâce à cette extraordinaire propriété géométrique, l’architecte de Vézelay est parvenu à intégrer dans son projet le rythme de la nef romane (voir le système des Tables de Vézelay).
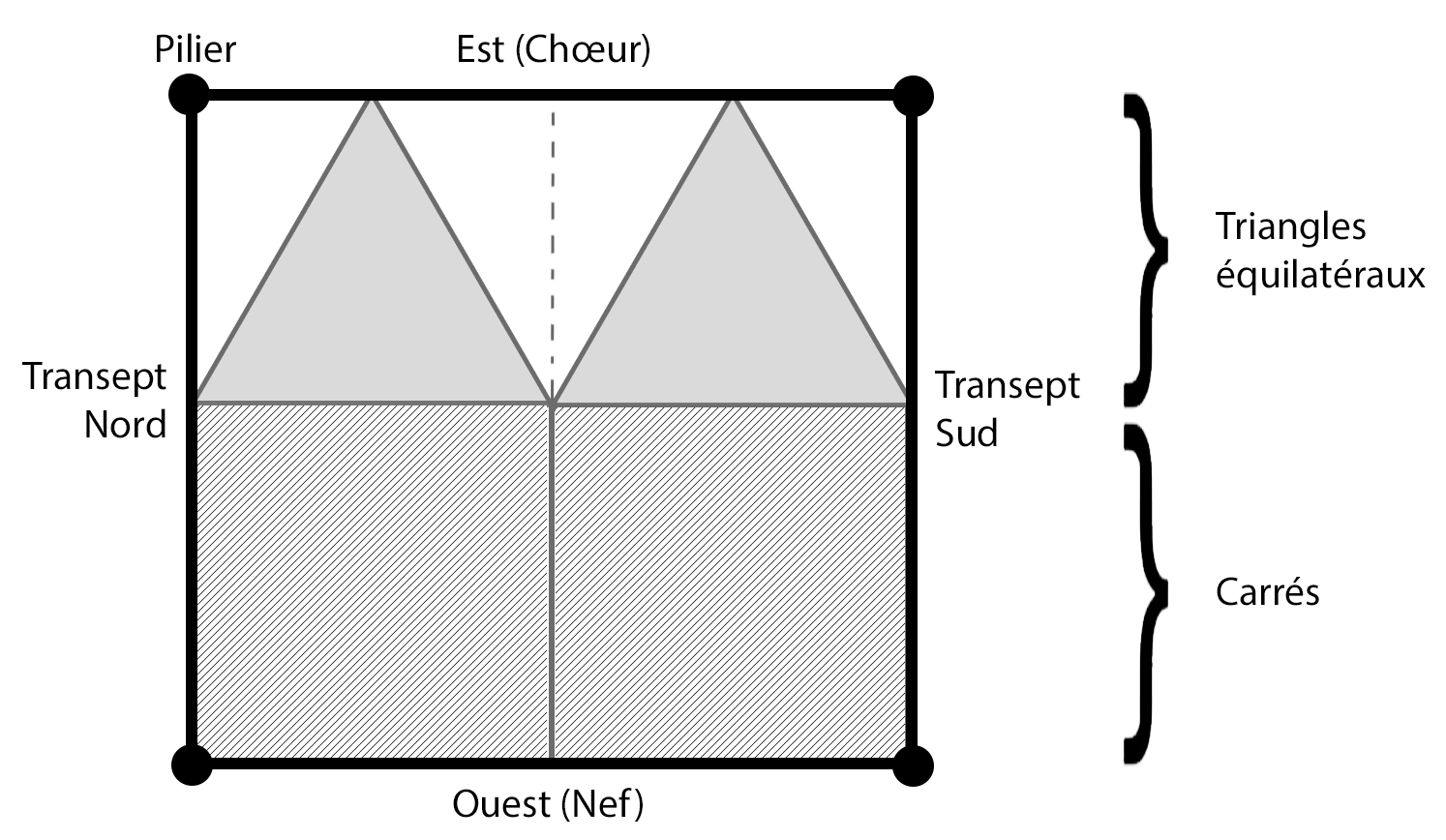
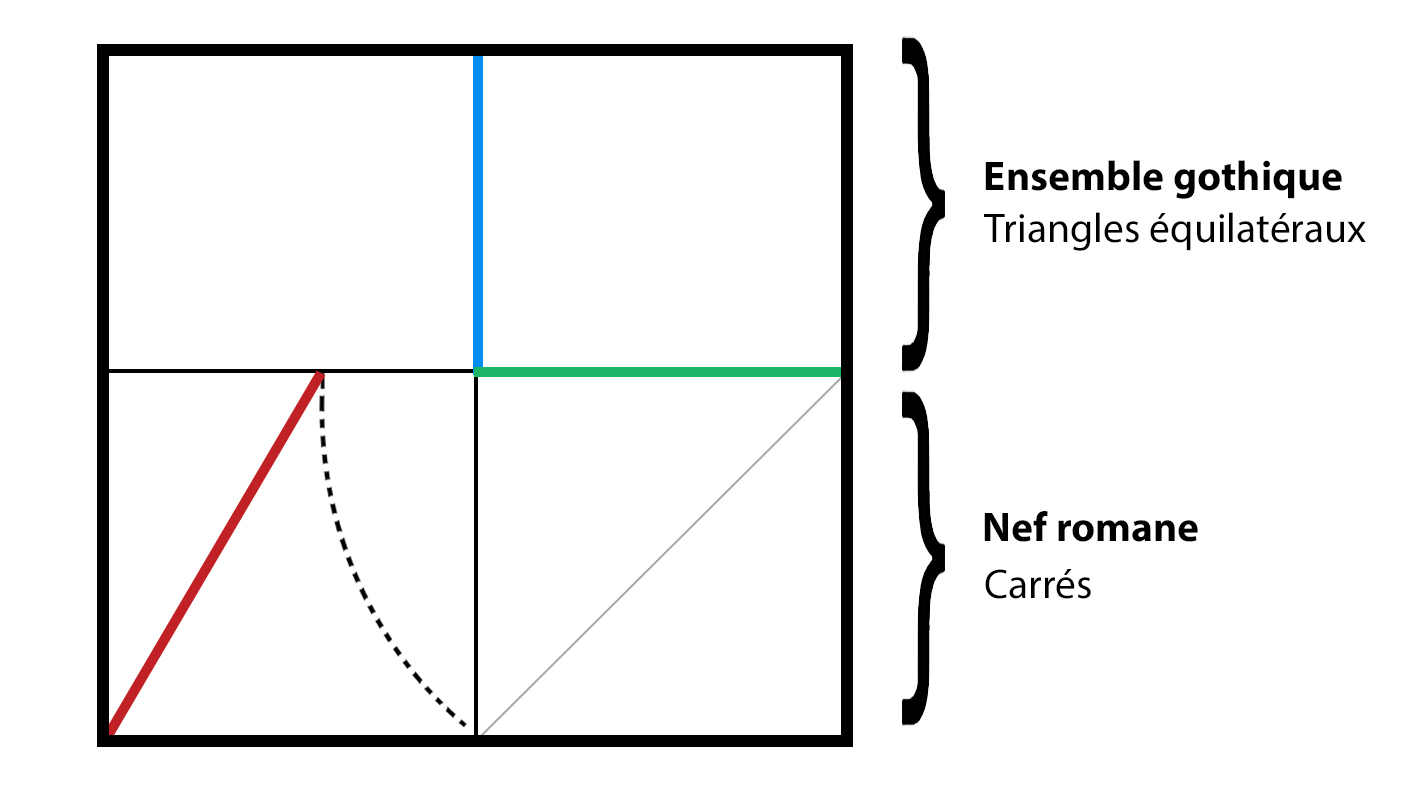
Tracé du plan de la basilique d’après Les clés de Vézelay.
Jean Pierre Bourcier - Budapest le 5 juillet 2019
Depuis la nuit des temps, toute épure commence de la même façon. Il faut tirer un trait carré pour définir deux axes de références. Alors supposons que le trait carré 11 - 22 de centre O soit tracé. Sur 11 est porté de part et d’autre de O la ½ largeur de la travée en OA et OB ; le cercle de rayon OA est tracé, il coupe 22 en N. L’intersection de deux arcs de cercles de rayon OA et de centre A et N et l’intersection de deux arcs de cercles de rayon OA et de centre B et N permet de définir les points C et D.

L’intersection de deux arcs de cercles de rayon OA de centre A et O ainsi que l’intersection de deux arcs de cercles de même rayon et de centre O et B définissent les points E et F.

La table peut alors être tracée.

L’arc de centre B et de rayon BG est tracé il coupe 11 en G1 ; le segment CG1 est tracé, il définit la largeur de la travée de la nef.

L’arc de cercle de centre C e de rayon CG1 est tracé, il coupe l’axe 22 en G3 et le prolongement de AC en G2.

Le triangle CG3G2 n’est pas équilatéral la perpendiculaire abaissée de G3 sur CG2 ne passant pas par le milieu M de CG2 écart de position du sommet pour une largeur de travée de 10 m est suivant 22 de 31mm ce qui est totalement négligeable par rapport aux dimensions du bâtiment et des outils de piquetage utilisés.


Cet écart est comparable à celui que l’on trouve dans le tracé du polygone du chœur, ici on ne privilégie pas l’exactitude mathématique du tracé, mais sa simplicité de réalisation, l’écart n’étant perceptible que pour l’initié.
Le report du segment AH en AH1 et H1H2 ainsi que le tracé symétrique par rapport à 22 permet de définir la deuxième et la troisième enceinte suivant la direction 11.
Le report du segment JK en JK1 et K1K2 ainsi que le tracé symétrique par rapport à 11 permet de définir la deuxième et troisième enceinte suivant la direction 22.

À partir de ce tracé, on peut alors tracer les travées de la nef et celle du chœur. À la travée n, on applique la routine de Villard ce qui permet de tracer complètement le chœur.

On obtient alors la répartition suivante :

Reste à tracer le narthex, suivant le tracé de la figure 5. Ce dernier présente une ambiguïté, car la longueur du rectangle est différente de la longueur du rectangle de la figure 6 qui est la largeur de la travée ; par rapport au plan donné de la basilique, les largeurs de travée narthex et nef sont identiques. D'autre part, il est précisé que l’architecte au travail va de l’autre côté de l’allée de la nef pour effectuer son tracé. On arrive donc à une largeur de travée narthex légèrement supérieure à la largeur travée nef ce qui semble se vérifier sur le plan.

L’ensemble de ces tracés est parfaitement réaliste, car il utilise des formes géométriques simples, carrés et triangles, faciles à tracer. Le nombre d’ouvertures de compas est de trois et seuls deux angles sont utilisés 45° et 60° (ou 30 son complément) éléments faciles à mémoriser.
Il n'est pas nécessaire de rappeler que beaucoup de tracés jusqu'à la fin du XIXe on fait l’objet de routines qui étaient mémorisées et dont la mise en application ne nécessitait pas la connaissance de leurs démonstrations, et ce, afin que les ouvriers puissent les utiliser simplement. Pour exemple les routines du fascicule de boucher en charpente en bois.
Et le nombre d’or dans tout cela ? Le mieux est d’envoyer un SMS à Nicolas Flamel avec copie au comte de St-Germain pour avoir la réponse.
Commentaires
La démonstration de Pierre Bellenguez sur la géométrie des cathédrales est absolument remarquable de simplicité et d'efficacité. Elle est très convaincante, et en plus, très élégante, ce qui est bon signe. L'architecte Viollet le Duc avait lui aussi proposé en son temps une hypothèse de géométrie sacrée en étudiant les coupes des cathédrales, mais ses résultats n'étaient pas très probants. Les points de ses figures tombaient un peu n'importe où et l'ensemble manquait de la clarté qui arrive toujours lorsqu'on a découvert le principe directeur d'un dessin. La démonstration de Pierre Bellenguez tient elle bien mieux la route. Elle est donc supérieure à celle de l'immense Viollet le Duc, ce n'est pas rien. Franchement bravo.
David Orbach (Architecte - Ingénieur structure - Enseignant à l’Université Populaire de Caen de Michel Onfray)
JE VOUS CONSEILLE SANS RÉSERVE la lecture du nouvel opus de Pierre Bellenguez, consacré au décryptage des tracés géométriques de la basilique de Vézelay. En seulement quelques dizaines de pages et d'illustrations, sans sombrer un seul instant dans les spéculations zozotériques et en s'appuyant notamment à très bon escient sur un schéma explicite du carnet de Villard de Honnecourt, l'auteur fournit au lecteur des clés immédiatement compréhensibles, limpides, de la compréhension géométrique de l'édifice.
Jean-Michel Mathonière - Directeur éditorial chez Éditions Dervy - Historien des compagnonnages
Dans son livre, Pierre Bellenguez, passionné d’architecture gothique, décrypte les constructions des bâtisseurs en se mettant dans la peau de ces derniers. A l’aide de différentes cathédrales gothiques françaises, il réfute des théories populaires sur ces édifices et démontre l’usage des figures géométriques dans ces bâtiments. Il s’intéresse également au symbolisme présent au cœur des cathédrales en analysant différents éléments architecturaux et historiques. Son œuvre nous a été particulièrement utile afin d’illustrer les méthodes géométriques des cathédrales gothiques [...]
Site : lescathedrales.wordpress.com
Un ouvrage extraordinaire où l’on ne fait pas de rapport entre la distance de la terre à la lune avec l’hypoténuse de la face de la pyramide en vraie grandeur, mais où les tracés sont opératifs […] car tout commence, quelle que soit l’épure […] en trait carré.
Jean-Pierre Bourcier - Spécialiste du trait
Pierre Bellenguez, déjà auteur d'un ouvrage sur les cathédrales, propose, avec ce livret, de découvrir l'univers de la basilique de Vézelay autrement, en essayant de comprendre comment celle-ci a été bâtie, quels symboles géométriques renferme-t-elle, en étudiant le portail et les symboles représentés. Un volume richement illustré (photos, plans, coupes, élévations) à lire d'urgence !
Olivier Petit - Médiéviste
Le Livre du Jour est : Les cathédrales retracées Les nombres régissent nos grands édifices. Pour bien le comprendre, il faut sortir ses outils de géomètre et chercher les proportions. Un travail méthodique et plein de bon sens dans les nefs, croisées et transepts, dans les absides et les chevets, et bien sûr dans les élévations. Une promenade qui nous conduit à Amiens, Vézelay, Beauvais, Chartres Bourges et Reims … Un bonheur d’ouvrage que nous devons à Pierre Bellenguez
Jean-François Lecompte - écrivain
Je recommande... Le superbe ouvrage Les cathédrales retracées pour tous les passionnés d'architecture gothique. Dans son livre, l'auteur Pierre Bellenguez nous dévoile le message caché derrière les plans des grandes cathédrales gothiques. À consommer sans modération !
Luciano Xavier - Maquettiste en cathédrales gothiques
Dans ce livre, je m'attendait à entendre beaucoup parler de géométrie sacrée, de traditions et de société secrète et bien pas du tout... Pour mon plus grand bonheur et mon plus grand plaisir, c'est un livre précis, sourcé, technique, néanmoins facile d'accès, qui permet à un néophyte d'aborder le sujet sans difficultés. L'auteur est très pédagogue, ça se lit tout seul. [...] Clairement, ce livre va véritablement m'aider pour mon travail sur les mystères des cathédrales. [...] Encore une fois je remercie chaleureusement Pierre Bellenguez pour son livre les cathédrales retracées.
Arcana Les Mystères du Monde - Youtubeur (Chaine Arcana)
Avis de lecteur (Priceminister) Beau et instructif. Ouvrage superbe avec d'abondantes illustrations en noir ou couleurs. Avec une simplicité communicative, l'auteur décrypte la science des bâtisseurs. Il réécrit avec clarté et à l'aide d'abondantes études personnelles les techniques qui ont permis cette révolution dans l'architecture. Loin d'être un remake de littératures courantes, c'est un beau livre à offrir ou à se faire offrir.
troph38
Le Mot du Jour est : « Encore Vézelay »? Un livret abondamment illustré sur la géométrie particulière de Vézelay vient d’être édité par Pierre Bellenguez. Ayant eu le privilège de le lire avant l’impression je vous le recommande, car compas en mains c’est de la belle ouvrage ! Les illustrations sont superbes et pédagogiques, alors, comme en plus c’est pas cher (15€), que ça s’achète en ligne et que ça tiendra dans le sac de plage, offrez-le-vous au plus vite !
Jean-François Lecompte - écrivain
J'ai lu votre livre d'une traite et vais bientôt le relire plus lentement. Merci et bravo, vous avez répondu à tellement de mes questions.
John Brown
Pierre Bellenguez explique très bien le sens de la géométrie des cathédrales en prenant appui sur la basilique de Vézelay, dans son ouvrage [...] Les cathédrales retracées : la science des bâtisseurs
Anthony CRESTIN - La géométrie et le mythe
Passionné d'architecture, Pierre Bellenguez a repris les mesures des cathédrales et compris comment les bâtisseur ont réussi ces exploits architecturaux. Aucun nombre magique, mais du bon sens, de la simplicité et de l'expérience.
Joël Supéry - Site tuskaland.com
Regard d'un passionné d'architecture médiévale sur l'architecture secrète des cathédrales et la géométrie gothique. Un ouvrage très utile pour notre projet #STEAMBuilders (https://steambuilders.eu/fr/) qui a pour objectif de fournir aux enseignants des outils et la pédagogie nécessaires à la mise en œuvre de l'approche innovante et pluridisciplinaire des STEAM par la manipulation et la reconstruction de techniques et de patrimoine historiques !
Asso Fermat-Science
J'ai bien reçu votre admirable livre "Les cathédrales retracées" et je vous en remercie. Étant passionné par l'architecture sacrée j'ai pu l'apprécier. Encore merci. Cordialement,
M. Moldovan
"Dans le sillage du livre "Les cathédrales retracées", Pierre Bellenguez nous entraîne dans une visite initiatique de la basilique de Vézelay, à la découverte des procédés géométriques utilisés par les moines bâtisseurs. Compas en main, il nous fait découvrir l’alphabet de ce livre de pierre, la fascinante science des anciens maîtres d’œuvre". La basilique de Vézelay, un incontournable... !
Catherine Leschenne









Après son magnifique ouvrage intitulé : " Les cathédrales retracées ", je vous recommande vivement de découvrir le nouvel opus de l'excellent Bellenguez Pierre, consacré au décryptage des tracés géométriques de la basilique de Vézelay.
Dominique Gury